Задание состоит из трех частей, первая и третья обязательны для выполнения, вторая выполняется по желанию студента. Срок сдачи задания — 17 октября.
Двоичное дерево задается следующей структурой:
typedef struct _t {
int data; /* данные в узле */
struct _t *left, *right; /* указатели на левого и правого сыновей */
} t;
t *root; /* корень дерева */
Таким образом, каждый элемент дерева содержит некоторые данные и два указателя
на потомков (на левого сына и на правого). Сам узел будем называть отцом
этих двух потомков. Определение дерева требует, чтобы у каждого узла, кроме корня,
был ровно один отец. Указатель на корень дерева хранится в переменной root,
она равна нулю, если дерево пусто.
Левым и правым поддеревьями узла t (t != 0) будем называть
деревья (возможно, пустые), корнями которых являются соответственно t->left и
t->right.
Основные операции на деревьях: поиск элемента, добавление элемента, удаление элемента. Для поиска элемента в произвольном бинарном дереве необходимо обойти все элементы этого дерева. Существует два основных способа обхода дерева: в глубину и в ширину.
Обход в глубину производится рекурсивно либо с использованием стека. В обоих случаях можно обходить узлы дерева в различной последовательности. Обход начинается от корня. Выделяют три наиболее важных порядка обхода в глубину:
В качестве примера рассмотрим следующее дерево:
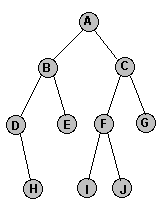
Запишем в качестве примера рекурсивную процедуру, выводящую на экран узлы дерева в порядке префиксного обхода.
void prefix(t *curr)
{
if (!curr)
return;
printf("%d ", curr->data);
prefix(curr->left);
prefix(curr->right);
}
Обход в ширину производится с помощью очереди. Первоначально в очередь помещается корень, затем, пока очередь не пуста, выполняются следующие действия:
Узлы дерева на рисунке перечисляются в порядке обхода в ширину следующим образом:
A, B, C, D, E, F, G, H, I, J. Заметим, что перечисление узлов происходит в порядке
удаления от корня, что делает поиск в ширину удобным, например, для поиска узла дерева
со значением k, наиболее близкого к корню, и т.д.
Приведем пример процедуры, которая выводит на экран узлы дерева в порядке обхода в ширину. Считаем, что определены три функции:
void add(t *elem); /* добавляет в конец очереди элемент elem */
t *del(); /* удаляет из очереди первый элемент и возвращает указатель на него */
int empty(); /* возвращает 1, если очередь пуста, и 0 в противном случае */
Тогда процедура обхода будет иметь следующий вид:
void width(t *root)
{
if (!root)
return;
add(root);
while (!empty()) {
t *curr = del();
printf("%d ", curr->data);
if (curr->left)
add(curr->left);
if (curr->right)
add(curr->right);
}
}
Пусть на множестве значений узлов дерева определена операция < (меньше). Будем называть двоичным деревом поиска двоичное дерево, удовлетворяющее следующему условию: для любого узла дерева все элементы левого поддерева меньше значения этого узла, а все элементы правого поддерева больше значения этого узла. Двоичные деревья поиска удобны для организации быстрого поиска данных, особенно в тех случаях, когда необходимо иметь возможность выдать данные в отсортированном виде. Для этого нужно всего лишь использовать инфиксный обход дерева.
Для поиска узла в таком дереве можно использовать как рекурсивную функцию, так и простой цикл.
Ниже приведен пример функции, которая ищет узел
со значением k в двоичном дереве поиска с корнем root. Этот код
весьма напоминает обычный бинарный поиск:
t *search(t *root, int k)
{
t *curr = root;
while (curr) {
if (k == curr->data)
return (curr);
if (k < curr->data)
curr = curr->left;
else
curr = curr->right;
}
return (0);
}
Добавление узла в двоичное дерево поиска напоминает добавление элемента в середину связанного списка: выполняется проход по дереву с запоминанием указателя на узел, предшествующий текущему, и добавление узла к предыдущему, как только текущий указатель станет равным нулю. Необходимо отдельно обработать случай пустого дерева.
Удаление узла из двоичного дерева поиска является менее тривиальной операцией: необходимо поддерживать выполнение условия расположения элементов («слева меньше, справа больше»). Одним из возможных способов является следующий:
При работе с двоичными деревьями поиска возможен случай, когда дерево по сути примет вид линейного связанного списка (например, если элементы подавались на вход в порядке возрастания). В таком случае поиск элемента в дереве будет занимать линейное время. Одним из способов предотвращения подобной ситуации является балансировка дерева по мере добавления элементов.
Сбалансированным деревом (AVL-деревом) называется двоичное дерево поиска, удовлетворяющее следующему условию: для любого узла глубина левого поддерева отличается от глубины правого поддерева не более чем на 1. В сбалансированном дереве поиск элемента выполняется за время O(log2N), где N — количество узлов (Адельсон-Вельский, Ландис, 1962). Алгоритм построения сбалансированных деревьев можно найти в сети и в литературе (Вирт, Кнут, ...), поэтому подробное описание его здесь не приводится.
Во входном файле input.txt в первой строке находится количество записей N,
в следующих N строках находятся записи вида имя значение, причем имена могут
повторяться. В файл output.txt выдать итоговые значения всех переменных в алфавитном
порядке. Хранение записей организовать в виде двоичного дерева поиска.
Ввод: input.txt
5
|
Вывод: output.txt
a 15
|
Задание аналогично предыдущему, но требуется поддерживать дерево сбалансированным. Задание не является обязательным.
Необходимо реализовать функции обхода дерева в порядке префиксного, инфиксного и постфиксного обходов. Дерево задается произвольным образом.